MIPS: Addressing and Decisions( Endereçamento e decisões)

Decisions in MIPS (decisões)


Instruction for decisions in MIPS( instruções de decisão) :

*  beq registo1, registo2, L1
*  beq means "branch if equal"

Same as (C): 
  if ( registo1== registo2) goto L1

Instruction supplementary decision in MIPS(Instrução de decisão complementar):

* bne registo1, registo2, L1
* bne means “branch if not equal”

Same as (C): 
  if ( registo1 != registo2) goto L1

"Goto" statement in MIPS(instrução "goto"):

It is the jump instruction ("jump") jumps directly to "label" indicated 

without checking any condition.

For example:

In C:

if (i == j) f=g+h; 

else f=g-h; 

 pseudo instruction                MIPS

if(condicion) goto TRUE;    beq $S3,$S4,TRUE
Code FALSE;                     sub $S0,$S1,$S2
goto NEXT;                         j NEXT
TRUE code TRUE;          TRUE
                                           add $S0,$S1,$S2
NEXT:                               NEXT


Another example:

In C:

do { 
g = g + A[i]; 
i = i + j;

} while (i != h); 

where g,h,i,j,base of A, $s1, $s2, $s3, $s4, $s5

pseudo instruction:

LOOP:  g=g+A[i]
             i=i+j;
             if(i!=h) goto LOOP;


MIPS:

LOOP : sll $St1,$S3,2 # St1=4*I
             //Construction of the vector
             add $t1,$t1,$S5  #St1=addr A[i] (address position for A[i])
              lw $t1,0($t1) # $t1=A[i]
             add $S1,$S1,$t1 # g= g+A[i]
             add $S3,$S3,$S4 # i=i+j
             bne $S3,$S2,LOOP # goto LOOP
                                               # if(i!=h)

Análise de complexidade algoritmica

Razões para análise algorítmica:
→prever o seu desempenho (performance)
→comparar algoritmos
→estabelecer garantias para o algoritmo (T(N)<=Tmax)
T(N)=tempo de execução dum algoritmo com input size=N
→perceber a base teórica subjacente
→evitar bugs de performance

Técnicas algorítmicas:
→dividir e conquistar
→programação dinâmica

Exemplo:
Procurar um valor num determinado vector
Int procuraValor (Int *v,Int n, Int val)
{Int i;
    For(i=0;i<n;i++)
       If(v[i]==val)
            Return i;
Return -1;
}

Num algoritmo com tamanho de n dados ,temos 3 situações:

→melhor caso(best case ): situação mais favorável em termos de configuração dos dados na entrada T(N)=B(N)
→pior caso (worst case): situação mais desfavorável T(N)=W(N)
→caso médio (average case): e determinado estatisticamente o número médio de operações básicas T(N)=A(N)

Int s=0; // está instrução e executada 1 vez
For(i=0;i<n;i++)
S=+v[i] Única Instrução que acede ao vector(modelo de custo usado nesta análise poderia por exemplo: considerar apenas as instruções se acesso ao vector(ler ou escrever))

estas instruções são executadas n vezes

Análise algoritmica

* Utilizar metodologias  e/ou técnicas de análise de desempenho de algoritmos com o objetivo de:

→prever a sua performance temporal e espacial
→comparar algoritmos entre si
→estabelecer garantias de desempenho
→perceber a base teórica subjacente
→evitar bugs de performance

Abordagem empírica

1)variar o tamanho dos dados da entrada n(regra :aumentar o tamanho n, multiplicando o por 2)
2)medir para cada valor de n, o tempo do algoritmo
3)tentar encontrar a lei (função) matemática que melhor se afasta aos dados. Para isso aplica-se regressão LINEAR aos dados log-log

Multiplicidade

* Os relacionamentos têm uma multiplicidade, que especifica o número de elementos de cada entidade que participam neles

Exemplo anterior:
- Sabe -se que um aluno só se pode inscrever em um só um "curso"
- Sabe-se que num "curso" se podem inscrever nenhum ou N alunos

Modelo E R

Modelo E R

* Representa apenas aspectos estáticos( entidades , os seus relacionamentos e a as propriedades de ambas)
* Destina-se a melhorar o conhecimento do utilizador sobre os dados

Entidade: qualquer objecto indentificavel , por exemplo: aluno,curso, cliente....

Propriedade: é informação/dado sobre uma dada entidade, como por exemplo: idade, nome, morada,...

Relacionamento: entidade que serve para ligar dias ou mais entidades, como por exemplo: frequenta, tem....

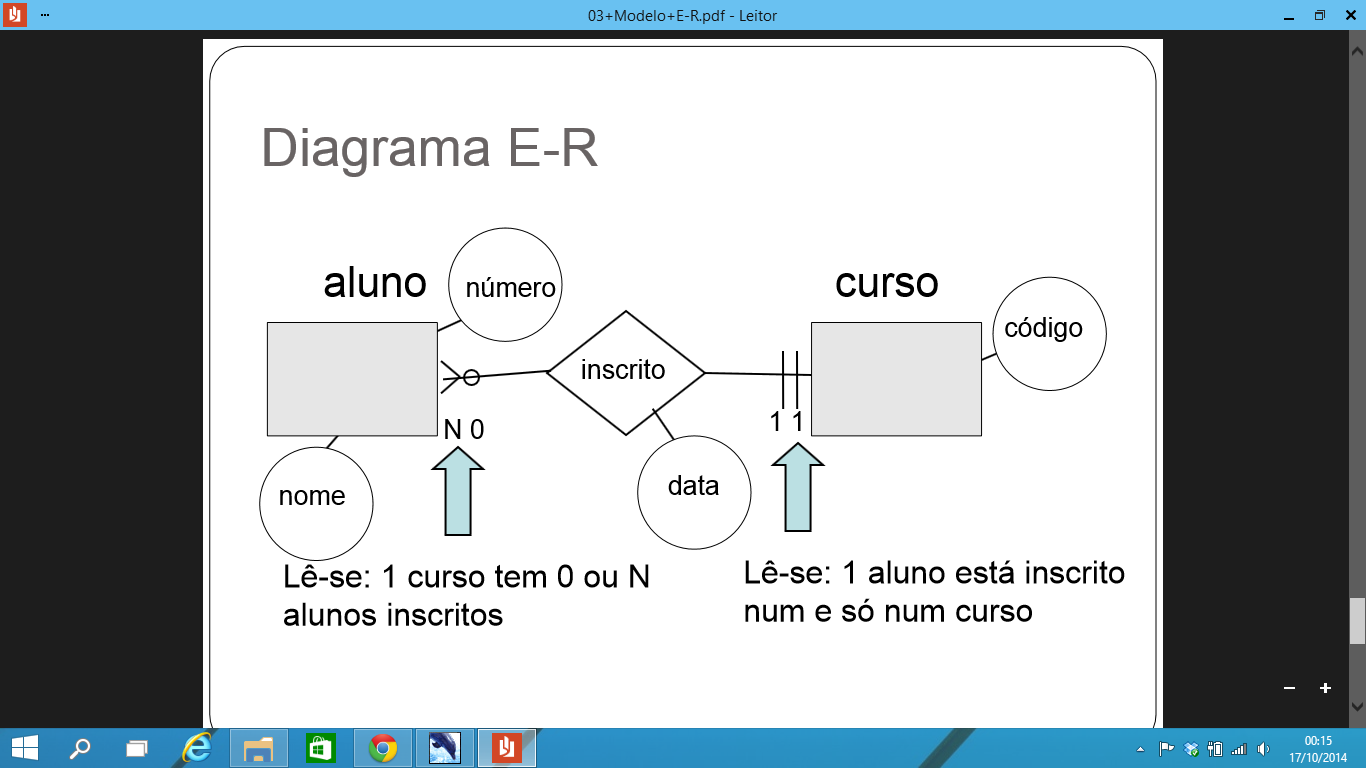
* Existe um relacionamento "inscrito" entre as entidade "aluno" e "curso"

* Esse relacionamento é caracterizado pelo atributo "data"

* As entidades "aluno" e "curso" têm os atributos mostrados